Recently, scientists at MIT released a "knotting secret". Not only do they tell you how to tie a knot, but they also tell you why.

From ancient times to the present, the human way of record-keeping has gone through the baptism of knots and oracle bones, lead and fire, pen and paper, light and electricity. According to Zhouyi, "In the ancient times, we knotted ropes and ruled, and in the later times, the sages changed the way of writing." It says that our old ancestors initially kept track of things by taking ropes as knots, and the shape and number of knots had an agreed-upon connotation, similar to legal documents. Later generations had oracle bones, silk, bamboo and wooden documents, and then paper.

The knot, a tangle of threads, has always played a seemingly small but important role in the development of human society. Not only the early memory, in modern times, climbers, navigators, construction workers, surgeons ...... can not do without the help of knots, mothers also rely on "knots" to knit the warmest sweater and the most beautiful Chinese knot.

But what kind of knot is the strongest? What is the best way to tie a knot so that we can safely deliver our lives?

What determines the strength of the knot?

Previously, the answer often came from a master, a friend or your own experience. But is experience always reliable? Is there a scientific rule that can effectively determine whether a certain knot is strong or not?

A new study recently published in Science by Jörn Dunkel et al. from the Massachusetts Institute of Technology (MIT) offers a viable solution to this problem.

The researchers did this by detailingAnalyzing the subtle interplay between the shape of the knot, elasticity, and friction, a suitable physical model was established and experimentally verified with a special rope that can change color as the force changes.

Rope that changes color with stress (top) and simulation results (bottom), which fit perfectly | Jörn Dunkel (paper author)

The results show thatTo determine whether a knot made of two ropes is secure, you need to focus on three factors: the number of points at which the ropes intersect, the torsional energy of the ropes, and the effect of tangential forces on the ropes.

In order to better understand the key points, the scientists gave concrete examples, accompanied by sketches. In this case, each rope is pulled at one end and "left alone" at the other to verify its stability - if the rope slips out easily, it means that the "knot" is not stable. The arrows in the diagram indicate the direction in which the rope was "pulled".

Now, let's take a look at these three factors and how they affect knot solidity.

1) Number of points where the ropes intersect

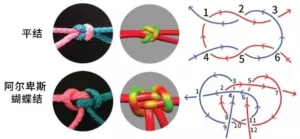
Flat and Alpine bows | Reproduced from Ref. 1

In the simplified line model, we can see that for the common "flat knot", the number of intersections of the two strands is 6, whereas the Alpine bow tie, which is commonly used by mountaineers, has 12 intersections, which is much more than the flat knot. Both people's experience and the simulation modeling and experimental results used in this study confirm thatWith more number of intersectionsThe Alpine Bow is much stronger than the Flat Knot.

Of course, they differ from each other by the following factors in addition to the number of intersecting points.

2) Torsional energy of the rope

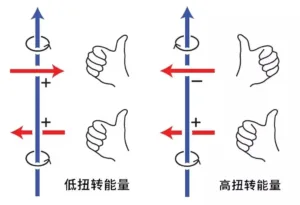
The rope at low torsional energy (left) and high torsional energy (right), with the former "spinning" like a chopstick being rolled and the latter "twisting" like a twist being rolled | Jörn Dunkel

Let's take the twisted state of the blue rope as an example. In the figure on the left, the blue string tends to rotate counterclockwise (like the "spinning" of chopsticks when you rub them together) due to the frictional forces exerted by the two red strings in different directions. The blue string tends to rotate more easily than it twists, i.e., it has a lower torsional energy.The knot has low torsional energy, is easy to spin and slip, and is less stable.

If the direction of one of the force is changed, as shown in the figure on the right, the effect of this force will then be changed to make the blue rope to produce the tendency to rotate clockwise. In this way, in the clockwise and counterclockwise rotation tendency of the joint action, the blue rope is easy to twist (similar to the twist, the twist of the kind of twist) but not easy to rotate, has a high torsion energy.Higher torsional energy of the knot makes it less likely to spin and slip, providing better safety.

Thus, in a complex knot, the knot is more robust when the combined effect of the directions of friction at the intersecting points gives the whole knot a higher torsional energy.

Let's take a flat knot and a very similar "grandmother's knot" as examples to get a feel for how torsional energy affects the stability of a knot.

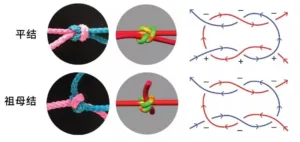
（Flat knot (with higher torsional energy) and grandmother knot (with lower torsional energy) | Reproduced from Ref. 1

As can be seen from the line model diagram above, the friction generated at the 3 intersections in the top half of the flat knot gives the blue rope a clockwise rotational tendency, while the 3 intersections in the bottom half cause it to rotate counterclockwise. For the grandmother's knot, the friction at all 6 intersections causes the blue rope to rotate clockwise, and the rope in this case is prone to rotational slippage. The same result can be obtained if the red rope is used as the object of study instead.

So.Despite having the same 6 intersections, the grandmother's knot is much less solid than the flat knot due to the difference in torsional energy.Mistaking a flat knot for a granny knot is a common mistake made by many novice climbers, and can even be dangerous, which is why granny knots are also jokingly referred to as "amateur flat knots".

3) Effect of tangential force on the rope

The torsional energy mentioned above is the interaction of vertical forces between the rope and the cord. And when the knot is pulled tight, the ropes are in close contact with each other, and the tangential forces they generate as they slide relative to each other in the direction of the rope cannot be ignored.

Consider two parallel ropes in close contact, pulled in opposite directions as opposed to the same direction, the friction will be greater and the knot they form will be more secure. Let's try to compare the flat knot with another "thief's knot" that is similar to the flat knot. The difference is that the flat knot has both ends of the force applied on the same side, whereas the thief knot has the force applied on the opposite side.

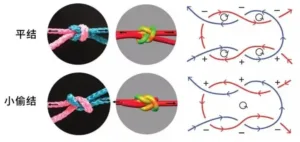
Flat and Thief knots (look exactly the same, but people pull and tug on them differently, refer to the black arrows in the picture on the left) | Reproduced from Ref. 1

As you can see from the simplified line model diagram, both the Flat Knot and the Thief Knot have 6 intersections and have the same torsional energy. However, experienced climbers will know that the Flat Knot has a better degree of solidity compared to the Thief Knot. The difference lies in the effect of the tangential force.

For the flat knot, the center section has an opposite pulling direction and the pulling direction is also opposite at the top and bottom 4 pairs of sections, while for the thief's knot, only the center section pulls in the opposite direction while the top and bottom 4 pairs of sections pull in the same direction.

So.The effect of tangential forces in the thief's knot is weaker and less secure than in the flat knot.This is probably the main reason why the thief's knot was only used by thieves for marking (the origin of the name "thief's knot") and not widely adopted by climbers.

Small studies, big applications

In this way, by analyzing the topology of the knot (a minimalist structure abstracted from solids, representing some "essential" feature) and obtaining the three important knot properties of the number of points of intersection of the ropes, the torsional energy, and the effect of the tangential force, we can qualitatively predict its solidity.

The scientists also found that of all the knots analyzed in this study, theSimulation and experimental results show that the "Zeppelin Knot" is the strongest and more secure than the Alpine Bow, which is popular in rock climbing.

Ultra Solid Zeppelin Knot | Reproduced from Ref. 1

 

This study provides a scientific and easy way to predict knot stability by analyzing knot shape characteristics.

bibliography

[1] V. P. Patil, J. D. Sandt, M. Kolle, J. Dunkel, Topologicalmechanics of knots and tangles, Science 367, 71-75 (2020).

[2] https://phys.org/news/2020-01-mathematical-stability.html

[3] https://www.npr.org/2020/01/02/793050811/a-knotty-problem-solved

[4] http://news.mit.edu/2020/model-how-strong-knot-0102

[5] https://www.sciencenews.org/article/color-changing-fibers-mysteries-math-physics-how-knots-work

[6] https://www.scientificamerican.com/article/color-changing-fibers-unravel-a-knotty-mystery/

This article is reproduced in the "Science Disinformation Platform" (ID: Science_Facts) public number, for reference only.